Informatik

Fünf »Informatik-Tricks«

• Paritätsbit
• Durch eine Karte sehen
• Eine Karte codieren
• Magische Tafeln
• Zauberwürfel

Quellenangaben
Lizenz

---

Paritätsbit

von Dorothee Müller (Quelle: »Computer Science Unplugged«, [Bell 2012])

Durchführung

Zunächst werden Objekte, die nur zwei verschiedene Zustände z₁, z₂ annehmen können, benötigt, wie zum Beispiel Magnetplättchen (»Rot« oder »Blau«) oder die von uns benutzten Fische (»auf dem Rücken schwimmen« oder »auf dem Bauch schwimmen«).

 

1. Ein Zuschauer legt die Fische mit beliebigem Zustand in einer m×n Matrix aus.
2. Ich lege eine weitere Spalte und eine weitere Zeile mit den Objekten genau so an, dass eine gerade Anzahl eines bestimmten Zustandes z₁ (z.B. gerade Anzahl »Fische auf dem Rücken«) in jeder Zeile und jeder Spalte ist.
3. Der Zuschauer dreht nun einen Fisch, ohne dass ich hinsehe.
4. Um den »Fehler« zu finden suche ich zeilenweise nach einer ungeraden Anzahl von z₁ (»Fische auf dem Rücken«). Ich merke mir diese Zeile j. Nun suche ich spaltenweise nach einer ungeraden Anzahl von z₁. Ich merke mir diese Spalte k. Das vom Zuschauer umgedrehte Objekt befindet sich in der j. Zeile und in der k. Spalte.

Material

Zweifarbige Magnetplättchen sind im Schulbedarf erhältlich. Der Trick kann auch mit anderen Elementen, die in einer Matrix angeordnet werden und zwei Zustande haben können, durchgeführt werden.

Zum Beispiel können Kreise und Kreuze an die Tafel gezeichnet werden. Für die Übung der Teilnehmenden haben wir Fische, die auf dem Rücken und dem Bauch schwimmend angeordnet werden konnten (siehe Bild rechts), verwendet: PDF.

Wie funktioniert das Ganze?

Mit dem Anfügen eines Paritätsbits für jede Zeile und Spalte einer binären Matrix wird redundante Information angefügt. Dadurch wird ein zweidimensionaler Fehlerkorrekturcode erschaffen, sodass man einen Fehler nicht nur finden, sondern auch den ursprünglichen Zustand der Bits wiederherstellen kann. Bei 2 oder 3 Fehlern können diese zwar erkannt, aber nicht mehr korrigiert werden. Sind 4 Fehler in der Matrix, so kann es passieren, dass diese nicht mehr erkannt werden.

Paritätsbits werden bei Datenübertragung und Datenspeicherung benutzt, um Fehler zu erkennen. Ein praktisches Beispiel ist die zerkratzte CD, bei der Kompression und Redundanz gleichzeitig angewendet werden und zu einer Fehlerkorrektur führen.

---

nach oben

Trick »Durch eine Karte sehen«

von Daniel Siebrecht (Quelle: »Die Magie der Informatik«, [Curzon 2005])

Durchführung

1. Ich habe ein Kartenspiel mit n Kartenⁱ.
2. Ich lasse das Publikum die Karten durchmischen.
3. Unter dem Vorwand offenlegen zu wollen, dass die Karten nun wirklich gut durchgemischt sind, zeige ich den Kartenstapel als Fächer. Dabei merke ich mir heimlich beim Zeigen eine der ersten Karten und deren Position x.
4. Nun lasse ich die Zuschauer eine Zahl y zwischen 1 und 10 wählenⁱⁱ.
5. Ich zähle y Karten vom Kartenstapel A abⁱⁱⁱ. Dann zähle ich 2x Karten ab und schließlich nochmals y Karten, sodass ich einen neuen kleineren Kartenstapel B mit 2x+2y Karten erhalte. Die Karte, die ich mir zu Beginn gemerkt habe, ist nun an Position x von unten im neuen Kartenstapel B.
6. Ich teile diesen Stapel B in 2 Hälften bzw. Teilstapel (C1 und C2), indem ich abwechselnd eine Karte von unten auf einen Stapel C1 und eine von oben auf einen Stapel C2 packe. C1 und C2 besitzen jeweils x+y Karten. Meine gemerkte Karte ist nun an Position x von unten in Stapel C1, d.h. an Position y+1 von oben.
7. Ich lege C2 auf A und C1 oben drauf.
8. Ich zähle y Karten ab.
9. Die nächste Karte ist die gemerkte. Ich kann sie scheinbar durch die Rückseite erkennen.

Material

Kartenspiel

Wie funktioniert das Ganze?

Der Bezug zur Informatik ist gegeben durch die Datenstruktur des Stapels. Die Karten stellen von Anfang an einen unsortierten Stapel dar, in dem die Position und der Inhalt eines Objektes bekannt ist. Durch verschiedene Operationen werden die Objekte des Stapels neu sortiert.

In der Realität existieren viele Beispiele für Datenstrukturen. Ein Kartendeck ist ein leicht verständliches Beispiel für einen Stapel.

1. Es muss gelten: n ≥ 2x + 2y. x und y werden im Anschluss erklärt.
2. Andernfalls wird der Zählaufwand zu groß.
3. A ist der gesamte Kartenstapel mit Größe n.

---

nach oben

Trick »Eine Karte codieren«

von Tabea Günther (Quelle: »Karten-Trick: 1 aus 5«, [Caduff 2007])

PDF

---

nach oben

Trick »Magische Tafeln«

von Klaus-Peter Watzlawek (Quelle: Die magischen Zahlen-Karten, [Sontheimer 2012])

Durchführung

1. Für den Trick werden zwei Spieler A und B benötigt.
2. A sucht sich im Stillen eine Zahl zwischen 1 und 100 aus.
3. Danach zeigt B ihm nacheinander die magischen Karten in ungeordneter Reihenfolge und fragt, ob die gemerkte Zahl auf der Karte ist.
4. B summiert die Zahl aus der linken oberen Ecke jeder Karte, auf der sich die Zahl befindet, auf.
5. Nach allen Karten hat B die Zahl von A berechnet.

Material

Die magischen Tafeln:

Alle Tafeln: [pdf] - [tex]

Wie funktioniert das Ganze?

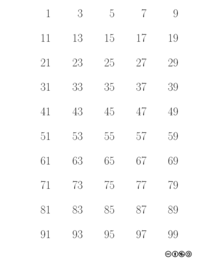
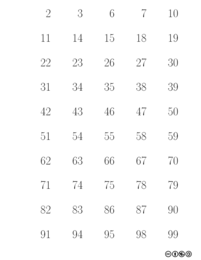
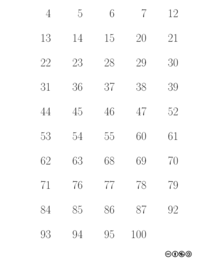
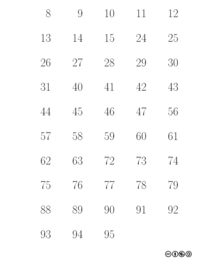
• Durch die Karten werden die Stellen einer Binärzahl kodiert. Es gibt 7 Karten, d. h. wir haben 7 Bit zur Verfügung.
• An Zahl in der linken oberen Ecke kann die Binärstelle der Karte in dezimaler Schreibweise abgelesen werden.
• Je nachdem wie der Gefragte antwortet, lässt sich durch das gesetzte Bit (Ja oder Nein) der jeweiligen Karte zum Schluss die Dezimalzahl durch Addition der Binärstellen bestimmen.

---

nach oben

Trick »Zauberwürfel«

von Dorothee Müller

Erklärung und Material

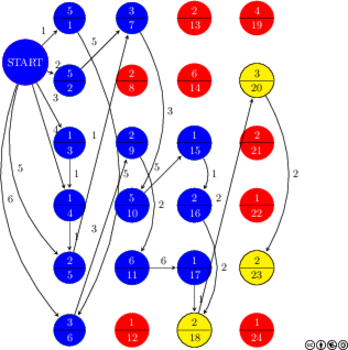
Übersicht und Spielfeld: [pdf] (Schwarz-Weiß) - [tex]

Spielfeld in Farbe: [pdf]

Wie funktioniert das Ganze?

Zur Erklärung des Spiels können die einzelnen Felder des Spielfeldes als Zustände in einem Automat aufgefasst und dadurch leicht erklärt werden: [pdf] [tex]. Weitere Hinweise zum mathematischen Hintergrund dieses Tricks können [Hàn 2008] entnommen werden.

---

nach oben

Quellenangaben/Verweise

Einige der vorgestellten Tricks wurden an bestehende Materialien angelehnt. Wir haben eine kleine Sammlung von Quellen und Verweisen auf weiterführende Inhalte/Materialien zusammengestellt:

• [Bell 2012] Bell, Tim; Witten, Ian H.; Fellows, Mike. Computer Science Unplugged, 2012. http://csedadmin.webfactional.com/books/.
  Weitere Hinweise zu »Computer Science Unplugged« können auch der Internetseite entnommen werden: http://csunplugged.org/.
• [Caduff 2007] Caduff, Otmar. Karten-Trick: 1 aus 5, 2007. SwissEduc: http://www.swisseduc.ch/informatik/diskrete_mathematik/kartentrick/index.html.
• [Curzon 2005] Curzon, Paul; McOwan, Peter; Black, Jonathan. Die Magie der Informatik, 2005. Queen Mary University of London. http://www.cs4fn.org/magie/.
• [Hàn 2008] Hàn, Hiệp. Markov Ketten, 2008. TU Berlin. http://www2.informatik.hu-berlin.de/alcox/lehre/lvss08/randalg/Markov_chains.pdf.
• [Sontheimer 2012] Sontheimer, Robert. Die magischen Zahlen-Karten, 2012. http://www.onlinewahn.de/karten.html.

---